编程中浮点数运算会损失精度已经成为了默认的惯例，精度损失的原因也信手拈来，目前科普文章大多讨论浮点数四则运算的精度问题，而鲜有探究其他浮点数运算的精度。

今天在做LeetCode 50的时候发现 LeetCode服务端检验的问题，同时带出了乘法运算和log、exp运算在硬件上的精度问题。

该题采用模拟的方式计算Pow，计算x的n次幂。测试过程中对于一些手动输入的样例不能通过，但是本题仍可以AC（考虑过double的问题）。

如图：
输入测试样例：

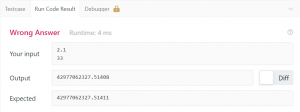
运行代码是LeetCode官方解答中的C++和Java的标程，运行结果均为：

小数点后几位精度有差别，导致WA

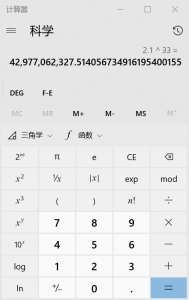
微软自带计算器的结果：

可见官方标程结果更接近

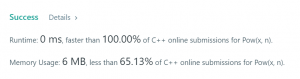
但是提交后仍然可以AC：

最后拿Java自带的Pow验证了一遍，结果是：42977062327.51411

C++自带的Pow结果是：42977062327.5141143799

可见LeetCode题解的模拟方式比自带的Pow更准（默认科学计算器是最准的）

这篇文章中指出Pow的实现方式是硬件的log和exp。

由此得出结论：

1. LeetCode服务器端用的是自带的Pow验证结果，而不是标程。
2. Pow的实现方式是硬件的log和exp，而不是本体题解的模拟乘法方式，模拟方式更准一点。
3. 乘法运算和log、exp运算的精度损失不一样，应该是硬件实现的问题。
4. 浮点数是真的不行。